Introduction to numpy

From ndarray to linalg
Published

January 23, 2024

NumPy is the fundamental package for scientific computing with Python. It contains among other things:

Besides its obvious scientific uses, NumPy can also be used as an efficient multi-dimensional container of generic data. Arbitrary data-types can be defined. This allows NumPy to seamlessly and speedily integrate with a wide variety of databases.

Library documentation: http://www.numpy.org/

The base numpy.array object

import numpy as np

# declare a vector using a list as the argument
v = np.array([1, 2.0, 3, 4])
v
array([1., 2., 3., 4.])
list([1, 2.0, 3, 4])
[1, 2.0, 3, 4]
type(v)
numpy.ndarray
v.shape
(4,)
v.ndim
1
v.dtype is float
False
v.dtype 
dtype('float64')
np.uint8 is int
False
np.array([2**120, 2**40], dtype=np.int64)
OverflowError: Python int too large to convert to C long
np.uint16 is int 
False
np.uint32
numpy.uint32
w = np.array([1.3, 2, 3, 4], dtype=np.int64)
w
array([1, 2, 3, 4])
w.dtype
dtype('int64')
a = np.arange(100)
type(a)
numpy.ndarray
np.array(range(100))
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16,
       17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
       34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
       51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
       68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84,
       85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99])
a
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16,
       17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
       34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
       51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
       68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84,
       85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99])
a.dtype
dtype('int64')
-3 * a ** 2
array([     0,     -3,    -12,    -27,    -48,    -75,   -108,   -147,
         -192,   -243,   -300,   -363,   -432,   -507,   -588,   -675,
         -768,   -867,   -972,  -1083,  -1200,  -1323,  -1452,  -1587,
        -1728,  -1875,  -2028,  -2187,  -2352,  -2523,  -2700,  -2883,
        -3072,  -3267,  -3468,  -3675,  -3888,  -4107,  -4332,  -4563,
        -4800,  -5043,  -5292,  -5547,  -5808,  -6075,  -6348,  -6627,
        -6912,  -7203,  -7500,  -7803,  -8112,  -8427,  -8748,  -9075,
        -9408,  -9747, -10092, -10443, -10800, -11163, -11532, -11907,
       -12288, -12675, -13068, -13467, -13872, -14283, -14700, -15123,
       -15552, -15987, -16428, -16875, -17328, -17787, -18252, -18723,
       -19200, -19683, -20172, -20667, -21168, -21675, -22188, -22707,
       -23232, -23763, -24300, -24843, -25392, -25947, -26508, -27075,
       -27648, -28227, -28812, -29403])
a[42] = 13
a[42] = 1025
np.iinfo(np.int16)
iinfo(min=-32768, max=32767, dtype=int16)
np.int16
numpy.int16
dict(enumerate(a))
{0: 0,
 1: 1,
 2: 2,
 3: 3,
 4: 4,
 5: 5,
 6: 6,
 7: 7,
 8: 8,
 9: 9,
 10: 10,
 11: 11,
 12: 12,
 13: 13,
 14: 14,
 15: 15,
 16: 16,
 17: 17,
 18: 18,
 19: 19,
 20: 20,
 21: 21,
 22: 22,
 23: 23,
 24: 24,
 25: 25,
 26: 26,
 27: 27,
 28: 28,
 29: 29,
 30: 30,
 31: 31,
 32: 32,
 33: 33,
 34: 34,
 35: 35,
 36: 36,
 37: 37,
 38: 38,
 39: 39,
 40: 40,
 41: 41,
 42: 1025,
 43: 43,
 44: 44,
 45: 45,
 46: 46,
 47: 47,
 48: 48,
 49: 49,
 50: 50,
 51: 51,
 52: 52,
 53: 53,
 54: 54,
 55: 55,
 56: 56,
 57: 57,
 58: 58,
 59: 59,
 60: 60,
 61: 61,
 62: 62,
 63: 63,
 64: 64,
 65: 65,
 66: 66,
 67: 67,
 68: 68,
 69: 69,
 70: 70,
 71: 71,
 72: 72,
 73: 73,
 74: 74,
 75: 75,
 76: 76,
 77: 77,
 78: 78,
 79: 79,
 80: 80,
 81: 81,
 82: 82,
 83: 83,
 84: 84,
 85: 85,
 86: 86,
 87: 87,
 88: 88,
 89: 89,
 90: 90,
 91: 91,
 92: 92,
 93: 93,
 94: 94,
 95: 95,
 96: 96,
 97: 97,
 98: 98,
 99: 99}
a + 1
array([   1,    2,    3,    4,    5,    6,    7,    8,    9,   10,   11,
         12,   13,   14,   15,   16,   17,   18,   19,   20,   21,   22,
         23,   24,   25,   26,   27,   28,   29,   30,   31,   32,   33,
         34,   35,   36,   37,   38,   39,   40,   41,   42, 1026,   44,
         45,   46,   47,   48,   49,   50,   51,   52,   53,   54,   55,
         56,   57,   58,   59,   60,   61,   62,   63,   64,   65,   66,
         67,   68,   69,   70,   71,   72,   73,   74,   75,   76,   77,
         78,   79,   80,   81,   82,   83,   84,   85,   86,   87,   88,
         89,   90,   91,   92,   93,   94,   95,   96,   97,   98,   99,
        100])
b = a + 1
b
array([   1,    2,    3,    4,    5,    6,    7,    8,    9,   10,   11,
         12,   13,   14,   15,   16,   17,   18,   19,   20,   21,   22,
         23,   24,   25,   26,   27,   28,   29,   30,   31,   32,   33,
         34,   35,   36,   37,   38,   39,   40,   41,   42, 1026,   44,
         45,   46,   47,   48,   49,   50,   51,   52,   53,   54,   55,
         56,   57,   58,   59,   60,   61,   62,   63,   64,   65,   66,
         67,   68,   69,   70,   71,   72,   73,   74,   75,   76,   77,
         78,   79,   80,   81,   82,   83,   84,   85,   86,   87,   88,
         89,   90,   91,   92,   93,   94,   95,   96,   97,   98,   99,
        100])
a is b
False
f = id(a)
a += 1
f, id(a)
(139656461862736, 139656461862736)
a
array([   1,    2,    3,    4,    5,    6,    7,    8,    9,   10,   11,
         12,   13,   14,   15,   16,   17,   18,   19,   20,   21,   22,
         23,   24,   25,   26,   27,   28,   29,   30,   31,   32,   33,
         34,   35,   36,   37,   38,   39,   40,   41,   42, 1026,   44,
         45,   46,   47,   48,   49,   50,   51,   52,   53,   54,   55,
         56,   57,   58,   59,   60,   61,   62,   63,   64,   65,   66,
         67,   68,   69,   70,   71,   72,   73,   74,   75,   76,   77,
         78,   79,   80,   81,   82,   83,   84,   85,   86,   87,   88,
         89,   90,   91,   92,   93,   94,   95,   96,   97,   98,   99,
        100])
b
array([   1,    2,    3,    4,    5,    6,    7,    8,    9,   10,   11,
         12,   13,   14,   15,   16,   17,   18,   19,   20,   21,   22,
         23,   24,   25,   26,   27,   28,   29,   30,   31,   32,   33,
         34,   35,   36,   37,   38,   39,   40,   41,   42, 1026,   44,
         45,   46,   47,   48,   49,   50,   51,   52,   53,   54,   55,
         56,   57,   58,   59,   60,   61,   62,   63,   64,   65,   66,
         67,   68,   69,   70,   71,   72,   73,   74,   75,   76,   77,
         78,   79,   80,   81,   82,   83,   84,   85,   86,   87,   88,
         89,   90,   91,   92,   93,   94,   95,   96,   97,   98,   99,
        100])

Warning

Beware of the dimensions: a 1D array is not the same as a 2D array with 1 column

a1 = np.array([1, 2, 3])
print(a1, a1.shape, a1.ndim)
[1 2 3] (3,) 1
a2 = np.array([1, 2, 3])
print(a2, a2.shape, a2.ndim)
[1 2 3] (3,) 1
a2.dot(a1) # inner product 
14
( np.array([a2])
     .transpose() # column vector
     .dot(
        np.array([a1])
     )
) # column vector multiplied by row vector
array([[1, 2, 3],
       [2, 4, 6],
       [3, 6, 9]])
np.array([a2]).transpose()#.shape
array([[1],
       [2],
       [3]])
(
    a2.reshape(3,1)  # all explicit
      .dot(a1.reshape(1, 3))
)
array([[1, 2, 3],
       [2, 4, 6],
       [3, 6, 9]])
# Declare a 2D array using a nested list as the constructor argument
M = np.array([[1,2], 
              [3,4], 
              [3.14, -9.17]])
M
array([[ 1.  ,  2.  ],
       [ 3.  ,  4.  ],
       [ 3.14, -9.17]])
M.shape, M.size
((3, 2), 6)
M.ravel(), M.ndim, M.ravel().shape
(array([ 1.  ,  2.  ,  3.  ,  4.  ,  3.14, -9.17]), 2, (6,))
# arguments: start, stop, step
x = (
     np.arange(12)
       .reshape(4, 3)
)
x
array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11]])
y = np.arange(3).reshape(3,1)

y
array([[0],
       [1],
       [2]])
x @ y, x.dot(y)
(array([[ 5],
        [14],
        [23],
        [32]]),
 array([[ 5],
        [14],
        [23],
        [32]]))
np.linspace(0, 10, 51)  # meaning of the 3 positional parameters ? 
array([ 0. ,  0.2,  0.4,  0.6,  0.8,  1. ,  1.2,  1.4,  1.6,  1.8,  2. ,
        2.2,  2.4,  2.6,  2.8,  3. ,  3.2,  3.4,  3.6,  3.8,  4. ,  4.2,
        4.4,  4.6,  4.8,  5. ,  5.2,  5.4,  5.6,  5.8,  6. ,  6.2,  6.4,
        6.6,  6.8,  7. ,  7.2,  7.4,  7.6,  7.8,  8. ,  8.2,  8.4,  8.6,
        8.8,  9. ,  9.2,  9.4,  9.6,  9.8, 10. ])
np.logspace(0, 10, 11, base=np.e), np.e**(np.arange(11))
(array([1.00000000e+00, 2.71828183e+00, 7.38905610e+00, 2.00855369e+01,
        5.45981500e+01, 1.48413159e+02, 4.03428793e+02, 1.09663316e+03,
        2.98095799e+03, 8.10308393e+03, 2.20264658e+04]),
 array([1.00000000e+00, 2.71828183e+00, 7.38905610e+00, 2.00855369e+01,
        5.45981500e+01, 1.48413159e+02, 4.03428793e+02, 1.09663316e+03,
        2.98095799e+03, 8.10308393e+03, 2.20264658e+04]))
import matplotlib.pyplot as plt

# Random standard Gaussian numbers
fig = plt.figure(figsize=(8, 4))
wn = np.random.randn(1000)
bm = wn.cumsum()

plt.plot(bm, lw=3)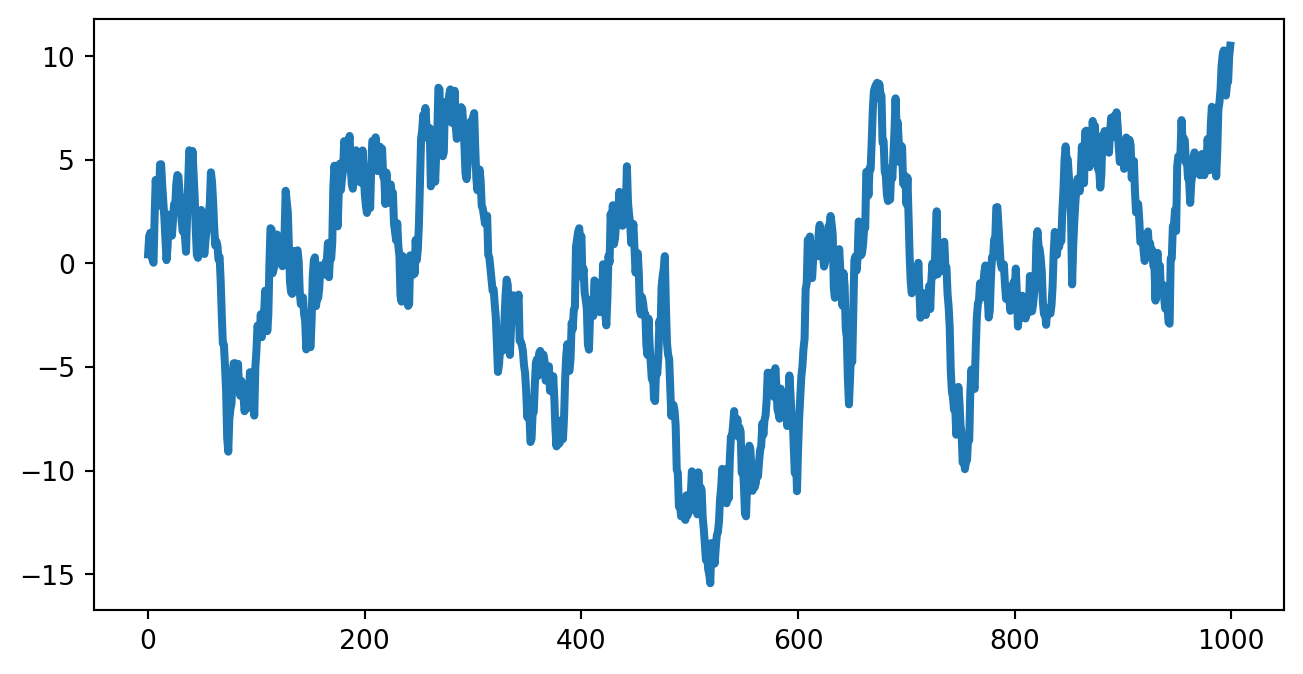

np.diag(np.arange(10))
array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 2, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 3, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 4, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 5, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 6, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 7, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 8, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0, 9]])
zozo = np.zeros((10, 10), dtype=np.float32)
zozo
array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]], dtype=float32)
zozo.shape
(10, 10)
print(M)
[[ 1.    2.  ]
 [ 3.    4.  ]
 [ 3.14 -9.17]]
M[1, 1]
4.0
# assign new value
M[0, 0] = 7
M[:, 0] = 42
M
array([[42.  ,  2.  ],
       [42.  ,  4.  ],
       [42.  , -9.17]])
M
array([[42.  ,  2.  ],
       [42.  ,  4.  ],
       [42.  , -9.17]])
# Warning: the next m is a **view** on M. 
# One again, no copies unless you ask for one!
m = M[0, :]
m
array([42.,  2.])
m[:] = 3.14
M
array([[ 3.14,  3.14],
       [42.  ,  4.  ],
       [42.  , -9.17]])
m[:] = 7
M
array([[ 7.  ,  7.  ],
       [42.  ,  4.  ],
       [42.  , -9.17]])

Slicing

# slicing works just like with anything else (lists, etc.)
A = np.array([1, 2, 3, 4, 5])
print(A)
print(A[::-1])
print(A[::2])
print(A[:-1:2])
[1 2 3 4 5]
[5 4 3 2 1]
[1 3 5]
[1 3]
[[n + m * 10 for n in range(5)] for m in range(5)]
[[0, 1, 2, 3, 4],
 [10, 11, 12, 13, 14],
 [20, 21, 22, 23, 24],
 [30, 31, 32, 33, 34],
 [40, 41, 42, 43, 44]]
A = np.array([[n + m * 10 for n in range(5)] for m in range(5)])
A
array([[ 0,  1,  2,  3,  4],
       [10, 11, 12, 13, 14],
       [20, 21, 22, 23, 24],
       [30, 31, 32, 33, 34],
       [40, 41, 42, 43, 44]])
print(A[1:4])
[[10 11 12 13 14]
 [20 21 22 23 24]
 [30 31 32 33 34]]
m = A[:, 1:4]
m[1, 1] = 123
A
array([[  0,   1,   2,   3,   4],
       [ 10,  11, 123,  13,  14],
       [ 20,  21,  22,  23,  24],
       [ 30,  31,  32,  33,  34],
       [ 40,  41,  42,  43,  44]])
A[1]
array([ 10,  11, 123,  13,  14])
A[:, 1]
array([ 1, 11, 21, 31, 41])
A[:, ::-1]
array([[  4,   3,   2,   1,   0],
       [ 14,  13, 123,  11,  10],
       [ 24,  23,  22,  21,  20],
       [ 34,  33,  32,  31,  30],
       [ 44,  43,  42,  41,  40]])
print(A)
[[  0   1   2   3   4]
 [ 10  11 123  13  14]
 [ 20  21  22  23  24]
 [ 30  31  32  33  34]
 [ 40  41  42  43  44]]
row_indices = np.array([1, 2, 4])
print(A[row_indices])
[[ 10  11 123  13  14]
 [ 20  21  22  23  24]
 [ 40  41  42  43  44]]
A[:, row_indices]
array([[  1,   2,   4],
       [ 11, 123,  14],
       [ 21,  22,  24],
       [ 31,  32,  34],
       [ 41,  42,  44]])

Another way is through masking with an array of bools

# index masking
B = np.arange(5)
row_mask = np.array([True, False, True, False, False])
print(B)
print(B[row_mask])
[0 1 2 3 4]
[0 2]
A, A[row_mask] , A[:,row_mask]
(array([[  0,   1,   2,   3,   4],
        [ 10,  11, 123,  13,  14],
        [ 20,  21,  22,  23,  24],
        [ 30,  31,  32,  33,  34],
        [ 40,  41,  42,  43,  44]]),
 array([[ 0,  1,  2,  3,  4],
        [20, 21, 22, 23, 24]]),
 array([[  0,   2],
        [ 10, 123],
        [ 20,  22],
        [ 30,  32],
        [ 40,  42]]))

Copies

Don’t forget that python does not make copies unless told to do so (same as with any mutable type)

If you are not careful enough, this typically leads to a lot of errors and to being fired !!

y = x = np.arange(6)
x[2] = 123
y
array([  0,   1, 123,   3,   4,   5])
x is y
True
# A real copy
y = x.copy()
x is y 
False
# Or equivalently (but the one above is better...)
y = np.copy(x)
x[0] = -12
print(x, y, x is y)
[-12   1 123   3   4   5] [  0   1 123   3   4   5] False

To put values of x in y (copy values into an existing array) use

x = np.random.randn(10)
x, id(x)
(array([ 0.22882628,  1.01836679,  1.02519228, -0.21674823,  0.77187089,
        -0.07460457,  1.17871761,  0.00135803,  1.06703629,  0.57036614]),
 139656462113488)
x.fill(2.78)   # in place. 
x, id(x)
(array([2.78, 2.78, 2.78, 2.78, 2.78, 2.78, 2.78, 2.78, 2.78, 2.78]),
 139656462113488)
x[:] = 3.14  # x.fill(3.14)  can. be chained ...
x, id(x)
(array([3.14, 3.14, 3.14, 3.14, 3.14, 3.14, 3.14, 3.14, 3.14, 3.14]),
 139656462113488)
x[:] = np.random.randn(x.shape[0])
x, id(x)
(array([-0.33509421,  0.6674441 ,  0.80431907,  1.23374741,  1.29200237,
        -0.72160291,  0.04892273,  0.70665894, -2.40541469, -0.92614552]),
 139656462113488)
y = np.empty(x.shape)  # how does empty() work ?
y, id(y)
(array([0.33509421, 0.6674441 , 0.80431907, 1.23374741, 1.29200237,
        0.72160291, 0.04892273, 0.70665894, 2.40541469, 0.92614552]),
 139656460714608)
y = x
y, id(y), id(x), y is x
(array([-0.33509421,  0.6674441 ,  0.80431907,  1.23374741,  1.29200237,
        -0.72160291,  0.04892273,  0.70665894, -2.40541469, -0.92614552]),
 139656462113488,
 139656462113488,
 True)

Final warning

In the next line you copy the values of x into an existing array y (of same size…)

y = np.zeros(x.shape)
y[:] = x
y, y is x, np.all(y==x)
(array([-0.33509421,  0.6674441 ,  0.80431907,  1.23374741,  1.29200237,
        -0.72160291,  0.04892273,  0.70665894, -2.40541469, -0.92614552]),
 False,
 True)

While in the next line, you are aliasing, you are giving a new name y to the object named x (you should never, ever write something like this)

y = x
y is x
True

Miscellanea

Non-numerical values

A numpy array can contain other things than numeric types

arr = np.array(['ou', 'là', 'là', ",ç'est", 'dur', 'python'])
arr, arr.shape, arr.dtype
(array(['ou', 'là', 'là', ",ç'est", 'dur', 'python'], dtype='<U6'),
 (6,),
 dtype('<U6'))
# arr.sum()
"_".join(arr)
"ou_là_là_,ç'est_dur_python"
arr.dtype
dtype('<U6')

A matrix is no 2D array in numpy

So far, we have only used array or ndarray objects

The is another type: the matrix type

In words: don’t use it (IMhO) and stick with arrays

# Matrix VS array objects in numpy
m1 = np.matrix(np.arange(3))
m2 = np.matrix(np.arange(3))
m1, m2
(matrix([[0, 1, 2]]), matrix([[0, 1, 2]]))
m1.transpose() @ m2, m1.shape, m1.transpose() * m2
(matrix([[0, 0, 0],
         [0, 1, 2],
         [0, 2, 4]]),
 (1, 3),
 matrix([[0, 0, 0],
         [0, 1, 2],
         [0, 2, 4]]))
a1 = np.arange(3)
a2 = np.arange(3)
a1, a2
(array([0, 1, 2]), array([0, 1, 2]))
m1 * m2.T, m1.dot(m2.T)
(matrix([[5]]), matrix([[5]]))
a1 * a2
array([0, 1, 4])
a1.dot(a2)
5
np.outer(a1, a2)
array([[0, 0, 0],
       [0, 1, 2],
       [0, 2, 4]])

Sparse matrices

from scipy.sparse import csc_matrix, csr_matrix, coo_matrix
probs = np.full(fill_value=1/4, shape=(4,))
probs
array([0.25, 0.25, 0.25, 0.25])
X = np.random.multinomial(n=2, pvals=probs, size=4)   # check you understand what is going on 
X
array([[1, 0, 0, 1],
       [1, 0, 0, 1],
       [0, 0, 0, 2],
       [1, 1, 0, 0]])
probs
array([0.25, 0.25, 0.25, 0.25])
X_coo = coo_matrix(X)  ## coordinate format
print(X_coo)
X_coo
  (0, 0)    1
  (0, 3)    1
  (1, 0)    1
  (1, 3)    1
  (2, 3)    2
  (3, 0)    1
  (3, 1)    1
<4x4 sparse matrix of type '<class 'numpy.int64'>'
    with 7 stored elements in COOrdinate format>
X_coo.nnz    # number pf non-zero coordinates 
7
print(X, end='\n----\n')
print(X_coo.data, end='\n----\n')
print(X_coo.row, end='\n----\n')
print(X_coo.col, end='\n----\n')
[[1 0 0 1]
 [1 0 0 1]
 [0 0 0 2]
 [1 1 0 0]]
----
[1 1 1 1 2 1 1]
----
[0 0 1 1 2 3 3]
----
[0 3 0 3 3 0 1]
----

There is also

  • csr_matrix: sparse rows format
  • csc_matrix: sparse columns format

Sparse rows is often used for machine learning: sparse features vectors

But sparse column format useful as well (e.g. coordinate gradient descent)

Bored with decimals?

X = np.random.randn(5, 5)
X
array([[ 1.90961279,  0.45025904,  0.93362367,  2.35155649,  0.58194797],
       [ 0.63258277, -0.088729  ,  0.63493499,  0.22867402,  0.15696287],
       [-1.45274264, -0.7438334 , -0.26355842,  0.89366631, -0.95255453],
       [-0.18452788, -1.49901081, -1.45384679,  0.1891478 , -0.24027981],
       [-1.08846102, -1.19436781,  0.72603139,  0.24786334, -0.6253346 ]])
# All number displayed by numpy (in the current kernel) are with 3 decimals max
np.set_printoptions(precision=3)
print(X)
np.set_printoptions(precision=8)
[[ 1.91   0.45   0.934  2.352  0.582]
 [ 0.633 -0.089  0.635  0.229  0.157]
 [-1.453 -0.744 -0.264  0.894 -0.953]
 [-0.185 -1.499 -1.454  0.189 -0.24 ]
 [-1.088 -1.194  0.726  0.248 -0.625]]

Not limited to 2D!

numpy arrays can have any number of dimension (hence the name ndarray)

X = np.arange(18).reshape(3, 2, 3)
X
array([[[ 0,  1,  2],
        [ 3,  4,  5]],

       [[ 6,  7,  8],
        [ 9, 10, 11]],

       [[12, 13, 14],
        [15, 16, 17]]])
X.shape
(3, 2, 3)
X.ndim
3

Aggregations and statistics

A = np.arange(42).reshape(7, 6)
A
array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11],
       [12, 13, 14, 15, 16, 17],
       [18, 19, 20, 21, 22, 23],
       [24, 25, 26, 27, 28, 29],
       [30, 31, 32, 33, 34, 35],
       [36, 37, 38, 39, 40, 41]])
A.sum(), 42 * 41 //2
(861, 861)
A[:, 3].mean(), np.mean (3 + np.arange(0, 42, 6))
(21.0, 21.0)
A.mean(axis=0)
array([18., 19., 20., 21., 22., 23.])
A.mean(axis=1)
array([ 2.5,  8.5, 14.5, 20.5, 26.5, 32.5, 38.5])
A[:,3].std(), A[:,3].var()
(12.0, 144.0)
A[:,3].min(), A[:,3].max()
(3, 39)
A.cumsum(axis=0)
array([[  0,   1,   2,   3,   4,   5],
       [  6,   8,  10,  12,  14,  16],
       [ 18,  21,  24,  27,  30,  33],
       [ 36,  40,  44,  48,  52,  56],
       [ 60,  65,  70,  75,  80,  85],
       [ 90,  96, 102, 108, 114, 120],
       [126, 133, 140, 147, 154, 161]])
A
array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11],
       [12, 13, 14, 15, 16, 17],
       [18, 19, 20, 21, 22, 23],
       [24, 25, 26, 27, 28, 29],
       [30, 31, 32, 33, 34, 35],
       [36, 37, 38, 39, 40, 41]])
# sum of diagonal
A.trace()
105

Linear Algebra

A = np.arange(30).reshape(6, 5)
v1 = np.arange(0, 5)
v2 = np.arange(5, 10)
A
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19],
       [20, 21, 22, 23, 24],
       [25, 26, 27, 28, 29]])
v1, v2
(array([0, 1, 2, 3, 4]), array([5, 6, 7, 8, 9]))
v1 * v2
array([ 0,  6, 14, 24, 36])
v1.dot(v2), np.sum(v1* v2)
(80, 80)
v1.reshape(5,1) @ v2.reshape(1,5)
array([[ 0,  0,  0,  0,  0],
       [ 5,  6,  7,  8,  9],
       [10, 12, 14, 16, 18],
       [15, 18, 21, 24, 27],
       [20, 24, 28, 32, 36]])

Inner products

# Inner product between vectors
print(v1.dot(v2))

# You can use also (but first solution is better)
print(np.dot(v1, v2))
80
80
A, v1
(array([[ 0,  1,  2,  3,  4],
        [ 5,  6,  7,  8,  9],
        [10, 11, 12, 13, 14],
        [15, 16, 17, 18, 19],
        [20, 21, 22, 23, 24],
        [25, 26, 27, 28, 29]]),
 array([0, 1, 2, 3, 4]))
A.shape, v1.shape
((6, 5), (5,))
# Matrix-vector inner product
A.dot(v1)
array([ 30,  80, 130, 180, 230, 280])
# Transpose
A.T
array([[ 0,  5, 10, 15, 20, 25],
       [ 1,  6, 11, 16, 21, 26],
       [ 2,  7, 12, 17, 22, 27],
       [ 3,  8, 13, 18, 23, 28],
       [ 4,  9, 14, 19, 24, 29]])
print(v1)
# Inline operations (same for *=, /=, -=)
v1 += 2
[0 1 2 3 4]

Linear systems

A = np.array([[42,2,3], [4,5,6], [7,8,9]])
b = np.array([1,2,3])
print(A, b, sep=2 * '\n')
[[42  2  3]
 [ 4  5  6]
 [ 7  8  9]]

[1 2 3]
# solve a system of linear equations
x = np.linalg.solve(A, b)
x
array([2.18366847e-18, 2.31698718e-16, 3.33333333e-01])
Note

Solving a system of linear equations can be done in many different ways, depending on the rank of matrix A.

  • If A is square and invertible, … choose \(A^{-1} \times b\)
  • If A is not invertible
    • If A has full column rank, return the unique minimizer of \(\| A z - b \|^2\)
    • If A does not have full column rank, return a minimizer of \(\| A z - b \|^2\) with minimal \(\ell_2\) norm.
A.dot(x)
array([1., 2., 3.])

Eigenvalues and eigenvectors

A = np.random.rand(3,3)
B = np.random.rand(3,3)

evals, evecs = np.linalg.eig(A)
evals
array([ 1.3153937 ,  0.55932771, -0.33618987])
evecs
array([[-0.58326142, -0.82699802,  0.18630866],
       [-0.36228081,  0.32274286, -0.77541192],
       [-0.72702045,  0.46033826,  0.60334521]])

Singular value decomposition (SVD)

Decomposes any real matrix \(A \in \mathbb R^{m \times n}\) as follows: \[ A = U \times S \times V^\top \] where - \(U\) and \(V\) are orthogonal matrices (meaning that \(U^\top \times U = I\) and \(V^\top \times V = I\)) - \(S\) is a diagonal matrix that contains the singular values in decreasing order

print(A)
U, S, V = np.linalg.svd(A)
[[0.82562092 0.42146713 0.1829056 ]
 [0.10875482 0.09517153 0.52079772]
 [0.35551885 0.82766939 0.61773909]]

Note that the above line implements unpacking

U.dot(np.diag(S)).dot(V)
array([[0.82562092, 0.42146713, 0.1829056 ],
       [0.10875482, 0.09517153, 0.52079772],
       [0.35551885, 0.82766939, 0.61773909]])
A - U @ np.diag(S) @ V
array([[-4.44089210e-16,  2.22044605e-16, -5.55111512e-17],
       [-1.24900090e-16, -1.94289029e-16,  0.00000000e+00],
       [-3.33066907e-16, -3.33066907e-16, -2.22044605e-16]])
# U and V are indeed orthonormal
np.set_printoptions(precision=2)
print(U.T.dot(U), V.T.dot(V), sep=2 * '\n')
np.set_printoptions(precision=8)
[[ 1.00e+00 -1.67e-16 -1.11e-16]
 [-1.67e-16  1.00e+00 -3.61e-16]
 [-1.11e-16 -3.61e-16  1.00e+00]]

[[1.00e+00 3.33e-16 1.11e-16]
 [3.33e-16 1.00e+00 2.22e-16]
 [1.11e-16 2.22e-16 1.00e+00]]

Exercice: the racoon SVD

  • Load the racoon face picture using scipy.misc.face()
  • Visualize the picture
  • Write a function which reshapes the picture into a 2D array, and computes the best rank-r approximation of it (the prototype of the function is compute_approx(X, r)
  • Display the different approximations for r between 5 and 100
# !pip3 install pooch
import numpy as np
from scipy.datasets import face
import matplotlib.pyplot as plt
%matplotlib inline

X = face()
type(X)
numpy.ndarray
plt.imshow(X)
_ = plt.axis('off')

n_rows, n_cols, n_channels = X.shape
X_reshaped = X.reshape(n_rows, n_cols * n_channels)
U, S, V = np.linalg.svd(X_reshaped, full_matrices=False)
X_reshaped.shape
(768, 3072)
X.shape
(768, 1024, 3)
plt.plot(S**2)  ## a kind of screeplot
plt.yscale("log")

def compute_approx(X: np.ndarray, r: int):
    """Computes the best rank-r approximation of X using SVD.
    We expect X to the 3D array corresponding to a color image, that we 
    reduce to a 2D one to apply SVD (no broadcasting).
    
    Parameters
    ----------
    X : `np.ndarray`, shape=(n_rows, n_cols, 3)
        The input 3D ndarray
    
    r : `int`
        The desired rank
        
    Return
    ------
    output : `np.ndarray`, shape=(n_rows, n_cols, 3)
        The best rank-r approximation of X
    """
    n_rows, n_cols, n_channels = X.shape
    # Reshape X to a 2D array
    X_reshape = X.reshape(n_rows, n_cols * n_channels)
    # Compute SVD
    U, S, V = np.linalg.svd(X_reshape, full_matrices=False)
    # Keep only the top r first singular values
    S[r:] = 0
    # Compute the approximation
    X_reshape_r = U.dot(np.diag(S)).dot(V)
    # Put it between 0 and 255 again and cast to integer type
    return X_reshape_r.clip(min=0, max=255).astype('int')\
        .reshape(n_rows, n_cols, n_channels)
ranks = [100, 70, 50, 30, 10, 5]
n_ranks = len(ranks)
for i, r in enumerate(ranks):
    X_r = compute_approx(X, r)
    # plt.subplot(n_ranks, 1, i + 1)
    plt.figure(figsize=(5, 5))
    plt.imshow(X_r)
    _ = plt.axis('off')
    # plt.title(f'Rank {r} approximation of the racoon' % r, fontsize=16)
    plt.tight_layout()

Read the docs!